Pickering Governor Construction, Working and Equations

Construction and working of Pickering Governor

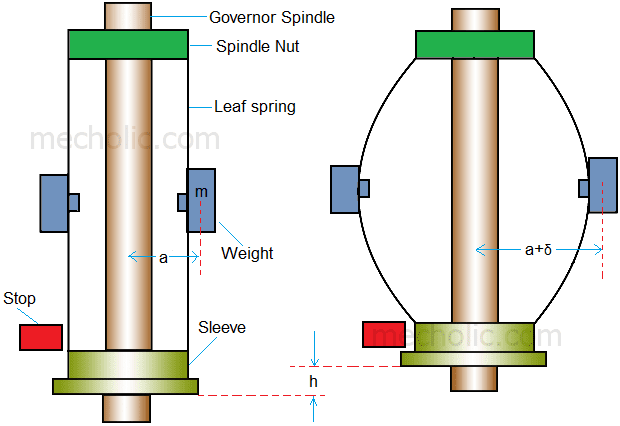
Pickering governor is very simple in construction and it is used for small machines. The sleeve movement in Pickering governor is very small when compared to the other centrifugal governor. It controls the speed by dissipating excess kinetic energy.


Pickering governor consists of three straight leaf spring each placed at equal angular interval around the spindle. The upper end of leaf spring attached to the hexagonal nut fixed to the governor spindle. The lower side of leaf spring attached to sleeve on the spindle which is free to slide on the spindle. Each of the spring carries a weight at its centre. When the speed of spindle increases the weight on the leaf spring tends to move outside. The governor leaf bends as the weight move outwards. When leaf spring bends, it lifts the leaf until it reaches the stop (stop position can be adjustable). Pickering governor found application in driving gramophone.

Pickering Governor equations for problem solving

From above figure,
m = Mass attached to each leaf spring
a = Distance between spindle axis to the centre of mass of weight when governor at rest
ω = Angular speed of the spindle
δ = Deflection of centre of leaf spring at angular speed ω
h = Lift of sleeve corresponding to the deflection δ
L = Distance between the fixed ends of the spring
E = Young’s modulus of the material of the spring
I = Moment of inertia of its cross-section about the neutral axis = bt³/12
(where b = width of spring and t = thickness of spring).

Lift of sleeve h ≈ 2.4 δ²/L

While the governor rotating the central load W is equal to the centrifugal force FC
W = FC = mrω² = m(a+ δ)ω²

The deflection of leaf spring carrying centre weight W when both sides are fixed is
δ = WL³/(192EI)

Apply W = m(a+ δ)ω² in above equation, we get
δ = m(a+ δ)ω²L³/(192EI)
The above equations are helpful to Pickering Governor problem solving