Different Types of Angles in Geometry Acute, Right, Obtuse, Straight, Reflex and Full Angle

What is an angle?

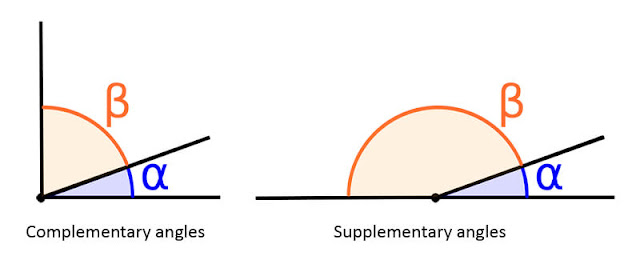
An angle is a measure of the amount of rotation between two lines or planes. It is defined as the amount of rotation needed to bring one line or plane into alignment with another. It shows how two lines or rays intersect. Angles are typically measured in degrees or radians and can be classified as acute, right, obtuse, straight, reflex, complementary, and supplementary based on their measure. Angles are a fundamental mathematical concept and have various applications in fields such as geometry, trigonometry, and physics. It is important to understand the different types of angles and their properties in these fields.

What are the parts of an angle?

An angle is a geometric shape that is formed by two rays that share a common endpoint, called the vertex. There are three main parts of an angle:

Vertex: The common endpoint of the two rays that form the angle.

Initial side: The first ray that forms the angle, also called the starting ray.

Terminal side: The second ray that forms the angle, also called the ending ray.

The measure of an angle is the amount of rotation between the initial side and the terminal side. The measure is usually given in degrees or radians.

The two rays that form an angle can be named in a number of ways, such as:

With a single letter, such as angle B, with the vertex at the point of the letter. With a point on each ray, such as angle ABC, with point A on the initial side, point B as the vertex and point C on the terminal side.

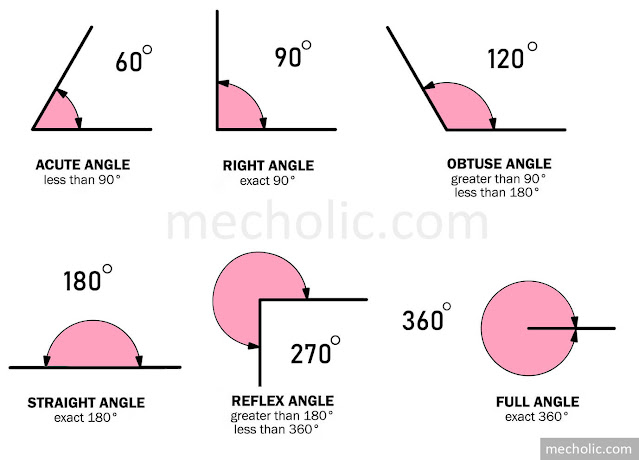
Six types of angles

Acute Angles: Acute angles are defined as angles that measure less than 90 degrees. It is considered the smallest type of angle.

Right Angles: A right angle is defined as an angle that measures exactly 90 degrees. Right angles are commonly found in construction, such as in the corners of buildings and bridges.

Obtuse Angles: Obtuse angles are defined as angles that measure greater than 90 degrees but less than 180 degrees. 

Straight Angles: A straight angle is defined as an angle that measures exactly 180 degrees. They are just a straight line.

Reflex Angles: Reflex angles are defined as angles that measure greater than 180 degrees but less than 360 degrees.

Full Angle: An angle that measures exactly 360 degrees. It is also worth noting that the measurement of angles is cyclical, meaning that after 360 degrees, the angle will start over again at 0 degrees.

 

🔗Angle measuring devices - Types of protractor

🔗Construction of sine bar how it measure angle

🔗Angle measurement and alignment using autocollimator

Positive angles and negative angles

Positive angles and negative angles are a way of describing the direction in which an angle is measured.

Positive angles are angles that are measured in a counterclockwise direction from the positive x-axis. This is the standard way of measuring angles in mathematics and physics. For example, an angle of 45 degrees would be considered a positive angle.

Negative angles, on the other hand, are angles that are measured in a clockwise direction from the positive x-axis. A negative angle of 45 degrees would be measured as 315 degrees, in a clockwise direction. A positive angle of 450 degrees is equivalent to a positive angle of 90 degrees.

In some cases, we use the direction of rotation to determine the angle. For example, when measuring the angle of rotation of a wheel or gear, a positive angle would indicate that the wheel or gear is rotating in a counterclockwise direction. In contrast, a negative angle would indicate that it is rotating in a clockwise direction.

In summary, positive angles are those measured in a counterclockwise direction from the positive x-axis and negative angles are those measured in a clockwise direction from the positive x-axis.

Types of angle pairs

Angle pairs refer to two or more angles that are related to each other in some way. There are several types of angle pairs, including:

Complementary and Supplementary angles: Complementary angles are two angles that add up to 90 degrees, while supplementary angles add up to 180 degrees. These angles play a key role in trigonometry and other branches of mathematics. They are used in various mathematical calculations and also in engineering designs.

🔗Clinometer types and equation

Adjacent angles: Two angles that share a common vertex and a common side, but have no other sides in common. These angles are considered adjacent.

Linear pair: Two angles that share a common vertex and a common side and whose non-common sides are opposite rays. A linear pair of angles are always supplementary.

Vertical angles: Two angles that are opposite each other when two lines intersect. They are congruent to each other.

Interior angle and Exterior angle: An interior angle is an angle that is located inside a polygon, while an exterior angle is an angle that is located outside a polygon. Two consecutive sides of the polygon form an interior angle of a polygon, and its measure is determined by the number of sides the polygon has. The sum of the measures of the interior angles of a polygon with n sides is equal to (n-2) x 180 degrees.

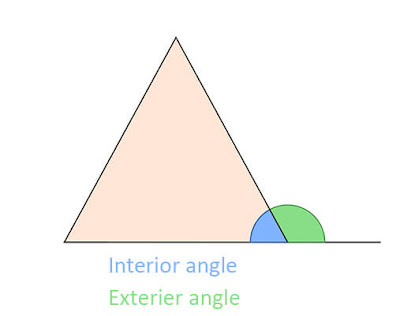
An exterior angle of a polygon is formed by the side of the polygon and an extended line that is not a side of the polygon. In any polygon, the sum of the exterior angles is always 360 degrees.

Alternate interior angles: Two angles that are located on the interior of two lines that are cut by a transversal and are on opposite sides of the transversal. They are congruent to each other.

Alternate exterior angles: Two angles that are located on the exterior of two lines that are cut by a transversal and are on opposite sides of the transversal. They are congruent to each other.

Corresponding angles: Two angles that are located on the same side of a transversal and are on corresponding positions of the two lines being cut. They are congruent to each other.