Sine Bar - Principle, Formula, Construction and Use
Sine bar is the one of the most accurate angle measuring device. sine bar used to measure an angle as well as locating a work-piece in required angle.
Construction details of sine bar
Sine bar consists of a precisely machined corrosion resistant chrome steel. It is essentially hardened and stabilized. It is resting on two identical hardened steel rollers. The distance between the centers of these rollers precisely controlled, this dimension is chosen to be a whole number (200mm, 250mm, 300mm, etc.) for easiness of angle calculation (this dimension becomes the hypotenuse in the calculation).The relief holes are drilled into the body of sine bar to reduce the weight, and to facilitate handling. Sine bar comes in different lengths, shape or design for the different application, but their principle is same.
Principle of sine bar and sine bar formula with diagram
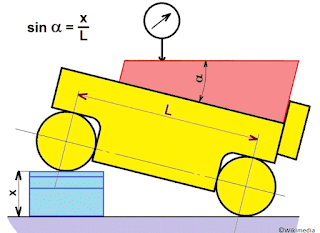
The above image shows the simplest arrangement of sine bar. To measure the angle a wedge is placed on flat surface. Sine bar is positioned on the wedge as shown in fig. Sine bar is supported on the roller on the gauge block. The top surface will incline the same angle as in the wedge. Now the sine of angle is equal to the ratio of the perpendicular distance between the rollers (H-h) to the horizontal distance between roller (length of sine bar, L). This is equivalent to the following figure. Now sine bar calculation formula can be written as following

Some other arrangement the object/ workpiece is placed top of the sine bar. Then a dial gauge probe is used to ensure the level of upper surface of workpiece.
Applications/use of sine bar
Sine bar application listed below- Checking flatness of a surface
- Locating a work in required angle.
- Checking angle of taper key
- Checking bevel gears
Difference between sine bar and protractor
The protractors measure the angle directly, whereas sine bar measures the angle
indirectly. Sine bar makes use of the trigonometric function to measure the angle. Sine bar it self not a complete measuring device, it cannot use alone for the measurement of angle. It uses along with auxiliary equipment such as gauge blocks and angle gauge sets. Sine bar has the capability of reducing all angle in terms of right angle.