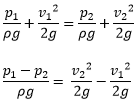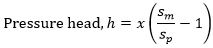Differential Pressure Flow Meter Working Principle (Derivation and Equation)
Read: Differential pressure flow meter - applications, advantages and limitations
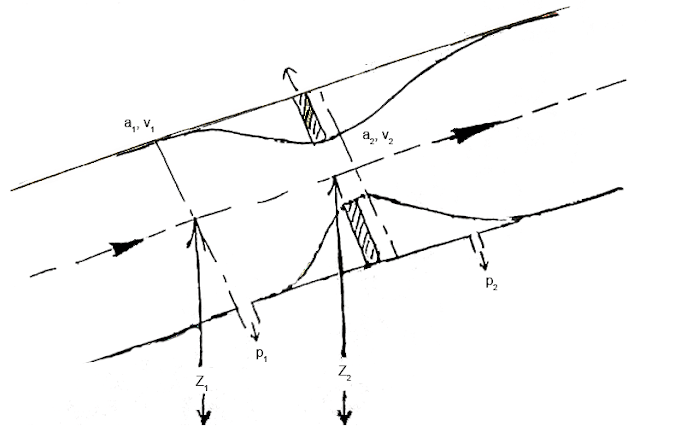
Assume a one-dimensional flow in through a restriction (venturi) fitted in a pipe. p, a,v,z are pressure, area, velocity, and elevation of fluid at a point respectively. According to the Bernoulli’s principle of conservation of energy total energy (total head) remains constant.
The first term of the above equation is called potential head or potential energy. The second term is called kinetic head or KE energy. This relationship between velocity and pressure provides the basis for the operation of all head type meters.
As the pipe is horizontal z1 = z2 or considering, the elevation is negligible z2-z1 = 0 the Bernoulli’s equation can be written as
The difference of the pressure head at section 1 and 2 is equal to “h.”
Substitute this value in the above equation we get
Now apply continuity equation at section 1 and 2
Substitute value of v1 in equation of h
The above equation gives theoretical discharge in ideal condition. The actual discharge will be less than theoretical discharge.
Cd is known as the coefficient of discharge and its value always less than 1
General theory for restriction type flow meter
Fig shows schematic representation of a one-dimensional flow system with restriction, Showing upstream 1 and downstream 2.Assume a one-dimensional flow in through a restriction (venturi) fitted in a pipe. p, a,v,z are pressure, area, velocity, and elevation of fluid at a point respectively. According to the Bernoulli’s principle of conservation of energy total energy (total head) remains constant.
The first term of the above equation is called potential head or potential energy. The second term is called kinetic head or KE energy. This relationship between velocity and pressure provides the basis for the operation of all head type meters.
As the pipe is horizontal z1 = z2 or considering, the elevation is negligible z2-z1 = 0 the Bernoulli’s equation can be written as
The difference of the pressure head at section 1 and 2 is equal to “h.”
Substitute this value in the above equation we get
Now apply continuity equation at section 1 and 2
Substitute value of v1 in equation of h
The above equation gives theoretical discharge in ideal condition. The actual discharge will be less than theoretical discharge.
Cd is known as the coefficient of discharge and its value always less than 1
- Difference between Differential Pressure Flow Meter and Positive Displacement Flow Meter
Let
Sm = specific gravity of the heavier fluid
Sp = specific gravity of the fluid in the pipe
X = manometer deflection
Then
Case 2: if the differential manometer contains lighter than the fluid in the pipeline.
Conversion of manometer deflection x to Pressure head difference h
Case 1: differential manometer contains liquid heavier than the liquid flowing through the pipeline.Let
Sm = specific gravity of the heavier fluid
Sp = specific gravity of the fluid in the pipe
X = manometer deflection
Then
Case 2: if the differential manometer contains lighter than the fluid in the pipeline.