Explain Fourier’s Law of Heat Conduction - Assumption, Essential Features and Equation

🔗Modes of Heat Transfer Conduction, Convection, Advection and Radiation

Assumptions of Fourier’s law

The Fourier's law based on the following assumption:

1. The material is homogeneous and isentropic, meaning that the value of thermal conductivity is constant in all direction.

2. Isothermal bounding surfaces.

3. Heat conduction takes place in the steady-state.

4. Heat flow is unidirectional (from higher temperature to lower).

5. Material has constant temperature gradient and linear temperature profile.

6. No internal heat generation.

Fourier's law of heat conduction

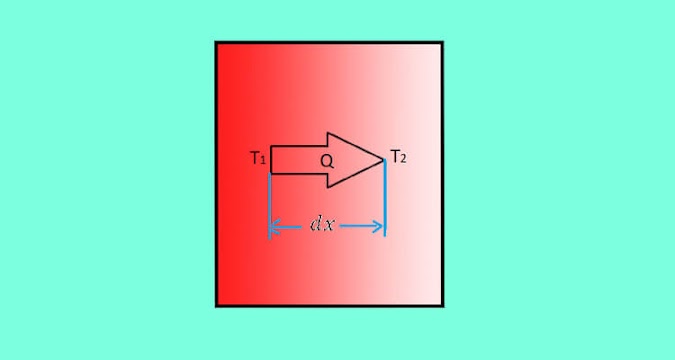
The rate of heat transfer through a homogeneous material is proportional to the area right angles to that gradient through which the heat flows and to the negative gradient in the temperature (change of temperature with respect to the distance of the heat flow)

Mathematically it can be represented as:

Here,

Q = Heat transfer through a body per unit time in watts (W)

A = Surface area section which is perpendicular to the direction of heat flow

∇T = Temperature gradient

dT = Temperature difference of body of thickness dx

dx = Thickness of body

k = Constant proportionality of material for heat conduction

Since temperature decrease along with the positive x-direction for heat conduction, the temperature gradient is always -ve. The -ve sign in the equation takes care of this, and the value of Q becomes positive.

Essential features of Fourier’s law of heat conduction

1. It is not an expression derived from the first principle; instead, it is based on experimental evidence.

2. It is a vector expression. -ve sign indicates that heat flow in the direction of decreasing temperature.

3. It is applicable to heat conduction in all materials regardless of their state (solid, liquid, gas).

4. It helps to determine the thermal conductivity ‘k’ of material through which heat transfer.