Addition And Subtraction of Vectors
Addition of Vectors
The addition of vectors refers to mathematically combining multiple vectors to determine a resultant vector. Adding individual vector quantities is essential for analyzing forces, accelerations, and other physics concepts.
Because vectors possess both magnitude and direction, they cannot be added using standard scalar arithmetic. Instead, vector addition must account for the directions using geometric rules. There are two primary methods for adding vectors - the triangle method and the polygon method.
Triangle Law of Addition of Vectors
The triangle, or tip-to-tail, method provides a straightforward technique for adding two vectors. For vectors A ⃗ and B ⃗:
- Draw vector A ⃗ to scale pointing in its proper direction.
- Draw vector B ⃗ with its tail at the head of vector A. This connects them tip-to-tail.
- Determine the magnitude and direction of the resultant vector C by drawing a line from the tail of A ⃗ to the head of B ⃗.
- Vector C ⃗ geometrically represents the sum of A ⃗ + B ⃗.
This method directly transfers the visual vector arrows into a graphical addition that automatically accounts for direction. The tip-to-tail method can also be done analytically using coordinate components.
To determine the magnitude of the resultant vector C ⃗, we can use the following equation:
Where
C is the magnitude of the resultant vector C ⃗
A is the magnitude of vector A ⃗
B is the magnitude of vector B ⃗
θ is the angle between vectors A ⃗ and B ⃗
The direction of the resultant vector C ⃗ makes an angle Φ with the first vector A ⃗. The tangent of this angle Φ is given by:
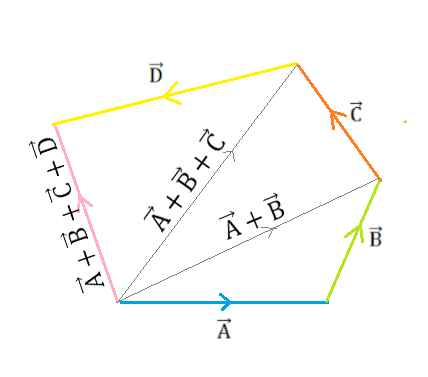
Polygon Method
The polygon method serves as an extension of the triangle method for adding three or more vectors:
- Select the first vector and draw it, pointing to its direction. This is the first side of the polygon.
- Draw the second vector tip-to-tail from the head of the first vector to form the second side.
- Draw all remaining vectors in tip-to-tail fashion, forming additional connected polygon sides oriented in the proper directions.
- Connect the original tail to the last vector tip to close the polygon. This final side depicts the resultant vector from adding all vectors.
By walking around this vector polygon, the path visually combines the vectors step-by-step based on the triangle law of vector addition. The closing line shows the net result. This provides a simple yet powerful technique for multi-vector addition problems.
Understanding vector addition methods provides the mathematical foundation for combining displacements, forces, velocities, and other physically meaningful vector quantities. Both geometric construction approaches offer a visualization for the vector summation process.
Subtracting Vectors
When subtracting two vectors A ⃗ and B ⃗, the process follows a method analogous to vector addition:
To subtract vector B ⃗ from vector A ⃗, we can represent this as the addition of vector A and vector -B ⃗. Here, vector -B ⃗ signifies vector B ⃗ that has been reversed 180 degrees in its direction.
For example, if vector -B ⃗ originally pointed north, vector -B ⃗ would be vector B pointing directly south, flipped completely around to point the opposite way. However, vector -B maintains the same magnitude as the original vector B ⃗.
So vector subtraction is carried out by adding the first vector A ⃗ to a reversed direction second vector -B ⃗. By flipping vector -B ⃗ to point in the opposite direction, adding it to A ⃗ yields the same result as if -B ⃗ was subtracted geometrically.
This technique of representing subtraction as addition with a reversed vector leads to the same end resultant. The tip-to-tail method or polygon method can then be applied using vector A ⃗ and reversed vector -B ⃗ to yield the overall vector difference through graphical addition.
The magnitude of